Помню, когда мы готовились к свадьбе, то достаточно много времени нам пришлось уделить для планировки рассадки гостей. У нас было около 50 человек и 8 столов. В итоге пришлось в фотошопе нарисовать столы в виде больших кругов, людей в виде маленьких и за пару вечеров, перетаскивая гостей мышкой туда-сюда, мы выбрали оптимальную рассадку. Тогда мне и пришла идея создать приложение, которое бы получало на вход информацию о гостях и столах, а на выходе бы давало самую оптимальную рассадку. В конце 2014 года я занялся этой задачей.
После некоторого анализа задачи я взглянул на нее как на задачу разделения графа: гости это узлы, их отношения между собой это ребра. Чем лучше отношения, тем больше вес ребра. Задача сводится к тому, чтобы разделить этот граф на определенное количество графов с заданным размером наилучшим образом. (сумма сумм всех ребер внутри графа максимальна).
Поигравшись с алгоритмами, я остановился на нижеописанном алгоритме. Чтобы рассказать о нём, надо договориться о некоторых формальностях:
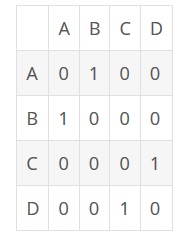
Надо рассадить их за два двухместных столика. Очевидно, что надо A посадить с B, а C с D. Суммарная оценка всех столов получиться 2.
Итак, об алгоритме. Суть его заключается в том, что сначала всех гостей садим за один большой стол, затем прикидываем как провести линию разреза, чтобы все были более-менее довольны и разделяем этот стол на две примерно равные по населенности части. Затем, с этими двумя новыми столами повторяем процедуру. Таким образом рано или поздно появится несколько столов нужной вместимости. Основная сложность — как разделить стол на две довольные половины. Делается это вот так:
Gij = -Mi + Ti — Mj + Tj — 2 Rij, где Rij это отношение между исследуемой парой.
Легко проверить, что физический смысл этого параметра — выгода суммарной оценки столов, которую можно получить, если поменять их i и j местами. Задача шага 3 — найти такую пару, что их G параметр будет максимален и положителен. В ином случае наилучшее разделение достигнуто.
Я реализовал API по этому алгоритму, исходный код которого можно посмотреть http://bitbucket.org/bryazginkos/seating-core/
На вход принимается xml файл. В нем описывается задача: гости, их отношения между собой и столы.
В ответ летит xml с решением. Все понятно из структуры.
Сложность алгоритма можно прикинуть сверху: это будет N*N*N*ln(S), где N — кол-во человек, S — количество столов.
Самая тяжелая часть алгоритма: поиск пар для обмена внутри одной итерации. Только поиск пары занимает N*N операций, за итерацию в худшем случае будет N обменов. И так для каждого разделения, число которых будет ln(S). Кстати, алгоритм распараллеливается.
Конечно, сразу как что-то более-менее заработало, я ввел туда гостей, которые были у нас на свадьбе и решил посмотреть, как алгоритм их рассадит. И тут я столкнулся со сложностью оценки отношений. Хочешь не хочешь, но надо установить, например, сколько хороших друзей заменят любимую девушку. Собственно, этот вопрос и остался открытым, я поигрался с различными оценками, получал различные варианты рассадки, в которых была своя логика, с которыми бы свадьба прошла на ура, но реальный вариант программа не угадала.
Свое любопытство я удовлетворил, поэтому, пока не занимаюсь этим проектом. Но я пришел к выводу, что для пользования алгоритмом нужно хорошее web приложение, которое поможет правильно расставить оценки отношений между людьми, при этом не замучав пользователя. На гитхабе https://github.com/bryazginkos/seating-web есть проект на gwtp — это оно и есть, но еще не законченное:)
После некоторого анализа задачи я взглянул на нее как на задачу разделения графа: гости это узлы, их отношения между собой это ребра. Чем лучше отношения, тем больше вес ребра. Задача сводится к тому, чтобы разделить этот граф на определенное количество графов с заданным размером наилучшим образом. (сумма сумм всех ребер внутри графа максимальна).
Поигравшись с алгоритмами, я остановился на нижеописанном алгоритме. Чтобы рассказать о нём, надо договориться о некоторых формальностях:
- Количество людей может быть меньше, чем количество мест за столами, поэтому, вводим «пустых» людей.
- Отношения между людьми оцениваем числом. Чем больше, тем лучше, допустимы отрицательные значения. Ноль — нейтральное.
- К «пустому» человеку все относятся нейтрально
- Для простоты все отношения симметричны.
- Оценкой стола будем называть сумму всех отношений между людьми за этим столом.
- Цель задачи — рассадить всех так, чтобы суммарная величина оценок всех столов была максимальна.
Надо рассадить их за два двухместных столика. Очевидно, что надо A посадить с B, а C с D. Суммарная оценка всех столов получиться 2.
Итак, об алгоритме. Суть его заключается в том, что сначала всех гостей садим за один большой стол, затем прикидываем как провести линию разреза, чтобы все были более-менее довольны и разделяем этот стол на две примерно равные по населенности части. Затем, с этими двумя новыми столами повторяем процедуру. Таким образом рано или поздно появится несколько столов нужной вместимости. Основная сложность — как разделить стол на две довольные половины. Делается это вот так:
- Разделяем стол на две примерно равные по количеству людей части случайным образом. (Необходимо разделять так, чтобы потом все «осколки» большого стола оказались столами, которые были даны в задаче.)
- Для каждого человека (пусть его номер будет i) считаем два параметра
- сумма всех его отношений к соседям по столу — обозначим как Mi
- сумма всех его отношений к людям с другого стола Ti
- Перебираем всевозможные пары людей (i, j) с разных столов, которые можно было бы пересадить. Для каждой пары считаем параметр Gij, который вычисляется по формуле:
Gij = -Mi + Ti — Mj + Tj — 2 Rij, где Rij это отношение между исследуемой парой.
Легко проверить, что физический смысл этого параметра — выгода суммарной оценки столов, которую можно получить, если поменять их i и j местами. Задача шага 3 — найти такую пару, что их G параметр будет максимален и положителен. В ином случае наилучшее разделение достигнуто.
- После нахождения пары с максимальным положительным G параметром, меняем их местами и помечаем, чтобы в последующих циклах их не трогали. Затем снова идем к шагу 2.
Я реализовал API по этому алгоритму, исходный код которого можно посмотреть http://bitbucket.org/bryazginkos/seating-core/
На вход принимается xml файл. В нем описывается задача: гости, их отношения между собой и столы.
<document>
<problem>
<Persons>
<Person id="7" name="Seven"/>
<Person id="16" name="Sixteen"/>
<Person id="1" name="One"/>
<Person id="14" name="Fourteen"/>
<Person id="4" name="Four"/>
<Person id="19" name="Nineteen"/>
<Person id="10" name="Ten"/>
<Person id="6" name="Six"/>
<Person id="9" name="Nine"/>
<Person id="11" name="Eleven"/>
<Person id="12" name="Twelve"/>
<Person id="13" name="Thirteen"/>
<Person id="5" name="Five"/>
<Person id="15" name="Fifteen"/>
<Person id="18" name="Eighteen"/>
<Person id="8" name="Eight"/>
<Person id="20" name="Twenty"/>
<Person id="2" name="Two"/>
<Person id="17" name="Seventeen"/>
<Person id="3" name="Three"/>
</Persons>
<Relations>
<Relation person1="1" person2="2" value="4"/>
<Relation person1="3" person2="4" value="2"/>
<Relation person1="3" person2="5" value="2"/>
<Relation person1="3" person2="6" value="2"/>
<Relation person1="4" person2="5" value="2"/>
<Relation person1="4" person2="6" value="2"/>
<Relation person1="5" person2="6" value="2"/>
<Relation person1="7" person2="8" value="2"/>
<Relation person1="7" person2="9" value="2"/>
<Relation person1="7" person2="10" value="2"/>
<Relation person1="8" person2="9" value="2"/>
<Relation person1="8" person2="10" value="2"/>
<Relation person1="9" person2="10" value="2"/>
<Relation person1="11" person2="12" value="2"/>
<Relation person1="11" person2="13" value="2"/>
<Relation person1="11" person2="14" value="2"/>
<Relation person1="12" person2="13" value="2"/>
<Relation person1="12" person2="14" value="2"/>
<Relation person1="13" person2="14" value="2"/>
<Relation person1="15" person2="16" value="2"/>
<Relation person1="15" person2="17" value="2"/>
<Relation person1="15" person2="18" value="2"/>
<Relation person1="15" person2="19" value="2"/>
<Relation person1="15" person2="20" value="2"/>
<Relation person1="16" person2="17" value="2"/>
<Relation person1="16" person2="18" value="2"/>
<Relation person1="16" person2="19" value="2"/>
<Relation person1="16" person2="20" value="2"/>
<Relation person1="17" person2="18" value="2"/>
<Relation person1="17" person2="19" value="2"/>
<Relation person1="17" person2="20" value="2"/>
<Relation person1="18" person2="19" value="2"/>
<Relation person1="18" person2="20" value="2"/>
<Relation person1="19" person2="20" value="2"/>
</Relations>
<Tables>
<Table capaciy="2" id="1"/>
<Table capaciy="4" id="2"/>
<Table capaciy="4" id="3"/>
<Table capaciy="4" id="4"/>
<Table capaciy="6" id="5"/>
</Tables>
</problem>
</document>
<document> <solving Estimation="70"> <Status id="0"/> <Tables> <Table capaciy="2" id="1"> <Persons> <Person id="1" name="One"/> <Person id="2" name="Two"/> </Persons> </Table> <Table capaciy="4" id="2"> <Persons> <Person id="7" name="Seven"/> <Person id="10" name="Ten"/> <Person id="9" name="Nine"/> <Person id="8" name="Eight"/> </Persons> </Table> <Table capaciy="4" id="3"> <Persons> <Person id="4" name="Four"/> <Person id="6" name="Six"/> <Person id="5" name="Five"/> <Person id="3" name="Three"/> </Persons> </Table> <Table capaciy="4" id="4"> <Persons> <Person id="12" name="Twelve"/> <Person id="13" name="Thirteen"/> <Person id="14" name="Fourteen"/> <Person id="11" name="Eleven"/> </Persons> </Table> <Table capaciy="6" id="5"> <Persons> <Person id="15" name="Fifteen"/> <Person id="18" name="Eighteen"/> <Person id="20" name="Twenty"/> <Person id="17" name="Seventeen"/> <Person id="16" name="Sixteen"/> <Person id="19" name="Nineteen"/> </Persons> </Table> </Tables> </solving> </document>
Самая тяжелая часть алгоритма: поиск пар для обмена внутри одной итерации. Только поиск пары занимает N*N операций, за итерацию в худшем случае будет N обменов. И так для каждого разделения, число которых будет ln(S). Кстати, алгоритм распараллеливается.
Конечно, сразу как что-то более-менее заработало, я ввел туда гостей, которые были у нас на свадьбе и решил посмотреть, как алгоритм их рассадит. И тут я столкнулся со сложностью оценки отношений. Хочешь не хочешь, но надо установить, например, сколько хороших друзей заменят любимую девушку. Собственно, этот вопрос и остался открытым, я поигрался с различными оценками, получал различные варианты рассадки, в которых была своя логика, с которыми бы свадьба прошла на ура, но реальный вариант программа не угадала.
Свое любопытство я удовлетворил, поэтому, пока не занимаюсь этим проектом. Но я пришел к выводу, что для пользования алгоритмом нужно хорошее web приложение, которое поможет правильно расставить оценки отношений между людьми, при этом не замучав пользователя. На гитхабе https://github.com/bryazginkos/seating-web есть проект на gwtp — это оно и есть, но еще не законченное:)

Комментариев нет :
Отправить комментарий